EJERCICIO 9 (Examen del Plan Antiguo Electrónica II Junio 2005/6 2ª Prueba Personal 2ª Semana).
Obtener la tabla de verdad de un circuito secuencial síncrono que funcione como un contador binario "up-down", (arriba_abajo), pero con las siguientes características:
- Su máximo valor de salida es 10.
- Su mínimo valor es 1.
- Se incremente de 1 en 1.
SOLUCIÓN:
Para realizar un contador "up-down" de módulo 10 (cuenta de 1 a 10) necesitamos una entrada de selección de contaje hacia arriba-abajo U y cuatro variables internas Q3, Q2, Q1 y Q0 para representar los 10 estados internos del contador.
1 Diagrama de estados del contador:
2 El número mínimo de biestables es 4, ya que el contador es de módulo 10 (23<10<24).
3 Si se realiza el contador con biestables JK, siendo sus transiciones:
| J | K | Q antes | Q después |
|---|---|---|---|
0 |
X |
0 |
0 |
1 |
X |
0 |
1 |
X |
1 |
1 |
0 |
X |
0 |
1 |
1 |
La tabla de excitación será la siguiente:
| ESTADOS | ENTRADAS t | SALIDAS t+1 | SALIDAS JK | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
U |
Q3 |
Q2 |
Q1 |
Q0 |
Q3 |
Q2 |
Q1 |
Q0 |
Estados |
J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 | |
I1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
I2 |
0 |
X |
0 |
X |
1 |
X |
X |
1 |
I2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
I3 |
0 |
X |
0 |
X |
X |
0 |
1 |
X |
I3 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
I4 |
0 |
X |
1 |
X |
X |
1 |
X |
1 |
I4 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
I5 |
0 |
X |
X |
0 |
0 |
X |
1 |
X |
I5 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
I6 |
0 |
X |
X |
0 |
1 |
X |
X |
1 |
I6 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
I7 |
0 |
X |
X |
0 |
X |
0 |
1 |
X |
I7 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
I8 |
1 |
X |
X |
1 |
X |
1 |
X |
1 |
I8 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
I9 |
X |
0 |
0 |
X |
0 |
X |
1 |
X |
I9 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
I10 |
X |
0 |
0 |
X |
1 |
X |
X |
1 |
I10 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
I1 |
X |
1 |
0 |
X |
X |
1 |
1 |
X |
I1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
I10 |
1 |
X |
0 |
X |
1 |
X |
X |
1 |
I2 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
I1 |
0 |
X |
0 |
X |
X |
1 |
1 |
X |
I3 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
I2 |
0 |
X |
0 |
X |
X |
0 |
X |
1 |
I4 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
I3 |
0 |
X |
X |
1 |
1 |
X |
1 |
X |
I5 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
I4 |
0 |
X |
X |
0 |
0 |
X |
X |
1 |
I6 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
I5 |
0 |
X |
X |
0 |
X |
1 |
1 |
X |
I7 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
I6 |
0 |
X |
X |
0 |
X |
0 |
X |
1 |
I8 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
I7 |
X |
1 |
1 |
X |
1 |
X |
1 |
X |
I9 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
I8 |
X |
0 |
0 |
X |
0 |
X |
X |
1 |
I10 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
I9 |
X |
0 |
0 |
X |
X |
1 |
1 |
X |
Se realizan las simplificaciones por mapa de Karnaugh de las salidas J y Kde cada biestable en función de las entradas U, Q0, Q1, Q2 y Q3.
Las ecuaciones lógicas de las entradas de los biestables son, por tanto:
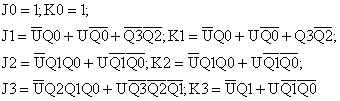
El circuito lógico es: