EJERCICIO 4 (Examen del Plan Antiguo Electrónica II Septiembre Reserva 2002/3 2ª Prueba Personal 2ª Semana).
Diseñe la tabla de fases y la de fusión de circuito de control para un semáforo, en el cual la secuencia de luces es: verde (64 segundos), amarillo (16 segundos), rojo (32 segundos), amarillo (8 segundos) y verde nuevamente. Dimensione todos los elementos que serán necesarios en la implementación.
SOLUCIÓN:
Se va a resolver el problema como un sistema secuencial síncrono, para ello se seguirán los siguientes pasos:
1) Identificación de las variables de entrada y salida.
La entrada será una señal de reloj que cada 8 segundos da un pulso, que se llamará X:
Entrada X
|
X = 0 cuando el reloj aún no ha llegado a 8 segundos |
X = 1 cuando el reloj ha llegado a 8 segundos |
Las salidas serán tres al igual que las luces del semáforo V (verde), R (rojo) y A (amarillo):
Salida V
|
Si V = 0 la luz verde está apagada |
Si V = 1 la luz verde está encendida |
Salida A
|
Si A = 0 la luz amarilla está apagada |
Si A = 1 la luz amarilla está encendida |
Salida R
|
Si R = 0 la luz roja está apagada |
Si R = 1 la luz roja está encendida |
2) Construcción del diagrama de estados y de la tabla de estados.
Si partimos del semáforo en verde, estado V1, mientras el pulso de 8 segundos no llegue a 8 la entrada será cero y permanecerá en el estado V1 (luz verde). Al llegar a los 8 segundos, la entrada será uno y del estado V1 se pasará al V2, con la luz verde. Al volver a uno la entrada, habrán pasado otros 8 segundos y se pasará al estado V3 (luz verde, pero sabemos que han pasado entre 16 y 23 segundos). Así, sucesivamente, hasta el estado V8 que al llegar el pulso a 8 segundos, ya han pasado 64 segundos y se pasará al estado A1 (luz en amarillo). Con dos estados en amarillo (A1 y A2) se tienen los 16 segundos que debe permanecer la luz del semáforo en amarillo. Del estado A2 se pasa al estado R1 (luz en rojo). Con cuatro estados en rojo (R1, R2, R3 y R4) se tienen los 32 segundos que debe permanecer la luz del semáforo en rojo. Del estado R4 se pasa al estado A (luz en amarillo). A los 8 segundos, del estado A se pasa a V1 de nuevo.
En el diagrama de estados con Modelo de Moore, se representan los estados internos y el valor de salida rodeados en un círculo. Sobre flechas se sitúan las transiciones entre estados internos, y sobre ellas se sitúa el valor de la entrada durante dicha transición. La salida depende sólo de las variables internas.
En el diagrama de estados con modelo de Mealy, se representan los estados internos rodeados por un círculo. Sobre las flechas, que representan las transiciones entre estados internos, se sitúa el valor que ha de tener la variable de entrada durante dicha transición y el valor de la salida. La salida depende de las variables internas y de las variables de entrada.
La tabla de estados es una representación, mediante una tabla, de la secuencia de estados por los que evoluciona el sistema. Los pasos a seguir para su construcción son los siguientes:
a) La tabla de fases tendrá tantas columnas como combinaciones de entrada del sistema, añadiendo las columnas por cada una de las salidas y una columna que indica el estado en el que se encuentra el sistema. En este problema se tiene una entrada que genera 2 combinaciones y tres salidas; por tanto se tienen 6 columnas.
b) Las filas de la tabla van creándose según van apareciendo nuevos estados. En cada fila se representa un sólo estado del circuito, mediante un número encerrado entre paréntesis, situado en la columna correspondiente a la combinación de variables de entrada que le dan lugar.
c) La salidas que produce dicho estado se escriben en la misma fila, en la columna de la salidas.
d) En la misma fila se escriben las transiciones a otros estados, que se producen cuando varían las entradas (éstas no pueden variar dos o más a la vez), con el mismo número del estado destino de la transición, pero sin encerrar entre paréntesis, y situados en la columna de la nueva combinación de entradas.
e) Cuando todas las transiciones vayan ya hacia estados anteriores, la tabla está completa.
Tabla de estados
| ESTADOS | ENTRADA X | SALIDAS | EXPLICACIÓN DE CADA ESTADO | |||
|---|---|---|---|---|---|---|
0 |
1 |
V |
A |
R |
||
V1 |
(V1) |
V2 |
1 |
0 |
0 |
semáforo en verde durante los 8 primeros segundos |
V2 |
(V2) |
V3 |
1 |
0 |
0 |
semáforo en verde durante los 8 a 16 segundos |
V3 |
(V3) |
V4 |
1 |
0 |
0 |
semáforo en verde durante los 16 a 24 segundos |
V4 |
(V4) |
V5 |
1 |
0 |
0 |
semáforo en verde durante los 24 a 32 segundos |
V5 |
(V5) |
V6 |
1 |
0 |
0 |
semáforo en verde durante los 32 a 40 segundos |
V6 |
(V6) |
V7 |
1 |
0 |
0 |
semáforo en verde durante los 40 a 48 segundos |
V7 |
(V7) |
V8 |
1 |
0 |
0 |
semáforo en verde durante los 48 a 56 segundos |
V8 |
(V8) |
A1 |
1 |
0 |
0 |
semáforo en verde durante los 56 a 64 segundos |
A1 |
(A1) |
A2 |
0 |
1 |
0 |
semáforo en amarillo durante los 8 primeros segundos |
A2 |
(A2) |
R1 |
0 |
1 |
0 |
semáforo en amarillo durante los 8 a 16 segundos |
R1 |
(R1) |
R2 |
0 |
0 |
1 |
semáforo en rojo durante los 8 primeros segundos |
R2 |
(R2) |
R3 |
0 |
0 |
1 |
semáforo en rojo durante los 8 a los 16 segundos |
R3 |
(R3) |
R4 |
0 |
0 |
1 |
semáforo en rojo durante los 16 a los 24 segundos |
R4 |
(R4) |
A |
0 |
0 |
1 |
semáforo en rojo durante los 24 a los 32 segundos |
A |
(A) |
V1 |
0 |
1 |
0 |
semáforo en amarillo durante los 8 segundos |
3) Fusión de la tabla de estados. Dos filas de la tabla de estados son fusionables si coinciden en sus columnas el número de los estados o estado y guión. No es necesario que coincidan sus salidas, aunque si esto ocurre, la salida depende sólo de los estados internos (Modelo de Moore). En la tabla de fusión, las columnas llevarán:
a) el número del estado con paréntesis si en alguna de las filas fusionadas este estado tenía paréntesis,
b) el número del estado sin paréntesis si en ninguna de las filas fusionadas este estado tenía paréntesis, pero aparece el número sin paréntesis,
c) guión si en todas las filas fusionadas hay guiones.
En este problema no hay posibilidad de fusionar la tabla de estados.
4) Codificación de estados internos. El número de variables internas (n) depende del número de filas de la tabla de fusión (N) cumpliéndose la siguiente expresión: 2n-1<N<=2n ; en este caso N=15 y por tanto, n=4, ya que 23=8 y 24=16.
Por tanto, la codificación de estados será la siguiente:
| ESTADOS | ENTRADA X | SALIDAS | VARIABLES INTERNAS | ||||||
|---|---|---|---|---|---|---|---|---|---|
0 |
1 |
V |
A |
R |
Q1 | Q2 | Q3 | Q4 | |
V1 |
(V1) |
V2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
V2 |
(V2) |
V3 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
V3 |
(V3) |
V4 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
V4 |
(V4) |
V5 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
V5 |
(V5) |
V6 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
V6 |
(V6) |
V7 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
V7 |
(V7) |
V8 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
V8 |
(V8) |
A1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
A1 |
(A1) |
A2 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
A2 |
(A2) |
R1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
R1 |
(R1) |
R2 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
R2 |
(R2) |
R3 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
R3 |
(R3) |
R4 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
R4 |
(R4) |
A |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
A |
(A) |
V1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
En un sistema real, es virtualmente imposible que dos variables cambien de valor en un mismo instante. Asignamos los valores de las variables internas de tal manera que al pasar de un estado a otro sólo una variable interna cambie. Pero al tener 15 estados y 16 combinaciones, al pasar del último estado A codificado con 1001 al primeroV1 codificado con 0000, cambiarían dos variables a la vez, lo cual es físicamente imposible, por lo que el sistema podría pasar del estado A 1001 a 0001 (V2) o a 1000 (estado no definido). Para que no suceda este fallo definimos el estado 1000 como una transición del estado A (1001) al V1 (0000). Así, a la tabla de codificación se cambia la última fila y se añade otra más.
Tabla de fusión codificada
| ESTADOS | ENTRADA X | SALIDAS | VARIABLES INTERNAS | ||||||
|---|---|---|---|---|---|---|---|---|---|
0 |
1 |
V |
A |
R |
Q1 | Q2 | Q3 | Q4 | |
V1 |
(V1) |
V2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
V2 |
(V2) |
V3 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
V3 |
(V3) |
V4 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
V4 |
(V4) |
V5 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
V5 |
(V5) |
V6 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
V6 |
(V6) |
V7 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
V7 |
(V7) |
V8 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
V8 |
(V8) |
A1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
A1 |
(A1) |
A2 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
A2 |
(A2) |
R1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
R1 |
(R1) |
R2 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
R2 |
(R2) |
R3 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
R3 |
(R3) |
R4 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
R4 |
(R4) |
A |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
A |
AV |
- |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
AV |
(AV) |
V1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
5) Tabla de excitación. Se construye a partir de la tabla de fusión codificada. Se colocan en cada fila cada uno de los estados estables y de transición que aparecen en la tabla de fusión codificada. En las columnas se tienen como entradas las entradas del sistema (X) y el valor de las variables internas en ese instante (Q1, Q2, Q3 y Q4); en las salidas están las salidas del sistema (S1, S2 y S3) y el valor de las variables internas al siguiente instante (Q1, Q2, Q3 y Q4). Se rellena la tabla con la combinación de esntradas y estados internos (Q) presente para cada estado (estable o de transición). En los estados estables la variable interna antes es igual a la variable interna después Qt+1 = Qt. En los estados de transición la variable interna cambia al valor que tendrá en su estado estable correspondiente.Por ejemplo, el estado de transición V2 tiene como entrada 1 y variables internas en la tabla de fusión codificada 0000, como su estado estable (V2) tiene como variables internas en la tabla de fusión codificada 0001; Qt será 0000 y Qt+1 será 0001 en la tabla de excitación.
En los estados estables las salidas tomarán el valor correspondiente de la tabla de estados. En los estados de transición se puede tomar el valor de la salida indiferente X (puede ser 0 ó 1) cuando se pase de un estado con salida diferente a la del anterior estado, ya que durará un tiempo corto (el que tarda en cambiar la variable interna Q) y dará lo mismo que la salida permanezca un poco más en 0 ó en 1. Pero, si la transición es entre dos estados con salida igual, la salida deberá permanecer en la transición igual, sino habría un cambio brusco en la salida que podría afectar al buen funcionamiento del circuito.
Por ejemplo, cuando el circuito pasa del estado estable (V8) (con salida S1=1) al estado estable (A1) (con salida S1=0), a través del estado de transición A1, dará igual que la salida en la transición A1 sea S1=1 (permaneciendo un pequeño tiempo más el semáforo en verde) o S1=0 (apagándose la luz verde). Es decir, en esta transición la salida S1 podría ser X. La salida S2 que pasa de ser 0 a 1 también podría ser X. Pero, todo esto podría producir en un instante de tiempo pequeño (transición A1) que las dos luces estén encendidas a la vez o estén apagadas a la vez. Para que no ocurra esto definimos las salidas S1 y S2 en las transiciones. Donde nunca podríamos poner X es en S3 que pasa de ser 0 a otra vez 0 y una X en la transición podría encender la bombilla roja un instante pequeño para volver a apagarse.
La tabla de verdad de los biestables JK es:
| J | K | Q antes | Q después |
|---|---|---|---|
0 |
X |
0 |
0 |
1 |
X |
0 |
1 |
X |
1 |
1 |
0 |
X |
0 |
1 |
1 |
Si utilizamos biestables JK para el circuito, tenemos la siguiente tabla de verdad para las variables internas:
| Estados | Entrada X | VARIABLES INTERNAS (antes) | VARIABLES INTERNAS (después)) | SALIDAS BIESTABLES JK | SALIDAS | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | Q4 |
Q1 | Q2 | Q3 | Q4 |
J1 |
K1 |
J2 |
K2 |
J3 |
K3 |
J4 |
K4 |
V |
A |
R |
||
(V1) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X |
0 |
X |
0 |
X |
0 |
X |
1 |
0 |
0 |
V2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
X |
0 |
X |
0 |
X |
1 |
X |
1 |
0 |
0 |
(V2) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
X |
0 |
X |
0 |
X |
X |
0 |
1 |
0 |
0 |
V3 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
X |
0 |
X |
1 |
X |
X |
0 |
1 |
0 |
0 |
(V3) |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
X |
0 |
X |
X |
0 |
X |
0 |
1 |
0 |
0 |
V4 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
X |
0 |
X |
X |
0 |
X |
1 |
1 |
0 |
0 |
(V4) |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
X |
0 |
X |
X |
0 |
0 |
X |
1 |
0 |
0 |
V5 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
X |
1 |
X |
X |
0 |
0 |
X |
1 |
0 |
0 |
(V5) |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
X |
X |
0 |
X |
0 |
0 |
X |
1 |
0 |
0 |
V6 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
X |
X |
0 |
X |
0 |
1 |
X |
1 |
0 |
0 |
(V6) |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
X |
X |
0 |
X |
0 |
X |
0 |
1 |
0 |
0 |
V7 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
X |
X |
0 |
X |
1 |
X |
0 |
1 |
0 |
0 |
(V7) |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
X |
X |
0 |
0 |
X |
X |
0 |
1 |
0 |
0 |
V8 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
X |
X |
0 |
0 |
X |
X |
1 |
1 |
0 |
0 |
(V8) |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
X |
X |
0 |
0 |
X |
0 |
X |
1 |
0 |
0 |
A1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
X |
X |
0 |
0 |
X |
0 |
X |
0 |
1 |
0 |
(A1) |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
X |
0 |
X |
0 |
0 |
X |
0 |
X |
0 |
1 |
0 |
A2 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
X |
0 |
X |
0 |
0 |
X |
1 |
X |
0 |
1 |
0 |
(A2) |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
X |
0 |
X |
0 |
0 |
X |
X |
0 |
0 |
1 |
0 |
R1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
X |
0 |
X |
0 |
1 |
X |
X |
0 |
0 |
0 |
1 |
(R1) |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
X |
0 |
X |
0 |
X |
0 |
X |
0 |
0 |
0 |
1 |
R2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
X |
0 |
X |
0 |
X |
0 |
X |
1 |
0 |
0 |
1 |
(R2) |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
X |
0 |
X |
0 |
X |
0 |
0 |
X |
0 |
0 |
1 |
R3 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
X |
0 |
X |
1 |
X |
0 |
0 |
X |
0 |
0 |
1 |
(R3) |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
X |
0 |
0 |
X |
X |
0 |
0 |
X |
0 |
0 |
1 |
R4 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
X |
0 |
0 |
X |
X |
0 |
1 |
X |
0 |
0 |
1 |
(R4) |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
X |
0 |
0 |
X |
X |
0 |
X |
0 |
0 |
0 |
1 |
A |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
X |
0 |
0 |
X |
X |
1 |
X |
0 |
0 |
1 |
0 |
AV |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
X |
0 |
0 |
X |
0 |
X |
X |
1 |
0 |
1 |
0 |
(AV) |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
X |
0 |
0 |
X |
0 |
X |
0 |
X |
0 |
1 |
0 |
V1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X |
1 |
0 |
X |
0 |
X |
0 |
X |
0 |
1 |
0 |
6) Ecuaciones lógicas de las salidas y de las variables internas. De la tabla de excitación se sacan los mapas de Karnaugh para la salidas S1, S2 y S3 y de las variables internas Q1, Q2, Q3 y Q4. Las entradas del mapa serán la entrada X y las variables internas Q1, Q2, Q3 y Q4.
Las ecuaciones lógicas son:
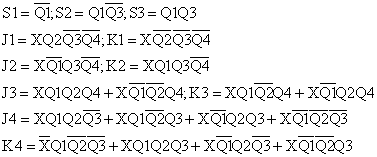
7) Circuito lógico. A partir de las ecuaciones lógicas obtenidas anteriormente, se obtiene el esquema del circuito lógico.