b)
c)
d)
EJERCICIO 14 (Examen del Plan Nuevo Electrónica Digital y Electrónica Básica Digital Junio 2006/7 2º Semana).
Tenemos el siguiente sistema secuencial representado por el diagrama de estados de la figura con una entrada X y unas variables de estado Q1 y Q2. Se pide obtener la tabla de excitación, las ecuaciones lógicas de salida y el circuito lógico.
Cuál de las siguientes expresiones no corresponde con la entrada que necesita el biestable de tipo T(Q1) del diagrama de estados anterior.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Sabiendo que D1 y D2 son las entradas que necesitan dos biestables de tipo D para responder de acuerdo al diagrama de estados anterior, indique cuál de las siguientes expresiones es cierta.
a) T1+T2 = 1
b) T1+D1 = 1
c) T1+D2 = 1
d) T1+T2 = D1+D2
Considerando que se han utilizado biestables tipo D en el diseño del sistema al que hace referencia el diagrama de estados anterior, indique cuál es la ecuación lógica de D1.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
SOLUCIÓN:
El diagrama de estado representa el funcionamiento de un circuito secuencial síncrono:
- Los estados internos del sistema, representados por las posibles combinaciones de las variables internas, están encerrados en un círculo. En nuestro problema hay cuatro estados internos diferentes representados por las combinaciones de Q1 y Q2 .
- Las transiciones o cambios en el circuito son las flechas que van de un círculo a otro. Estas transiciones se producen en cada señal de reloj.
- Sobre cada flecha se anota la combinación de entradas en la transición y, separadas por una barra, las salidas. En nuestro problema hay una entrada X.
Hay 4 estados inestables o transiciones (cambia el estado con cada señal de reloj) y un estado estable ( se mantiene el estado aunque se vayan produciendo impulsos de reloj):
- Estado de transición 2, partiendo del estado 1 con variables internas (instante t) Q1=0 y Q2=0 se pasa al estado 2 con variables internas (instante t+1) Q1=0 y Q2=1 si a la señal de reloj la entrada X vale 0. Es decir, del estado interno 00 pasamos al 01 cuando X=0.
También se produce una transición al estado 2, partiendo del estado 4 con variables internas (instante t) Q1=1 y Q2=1 se pasa al estado 2 con variables internas (instante t+1) Q1=0 y Q2=1, si a la señal de reloj la entrada X vale 0. Es decir, del estado interno 11 pasamos al 01, cuando X=0.
- Estado de transición 3, partiendo del estado 2 con variables internas (instante t) Q1=0 y Q2=1 se pasa al estado 3 con variables internas (instante t+1) Q1=1 y Q2=0, si a la señal de reloj la entrada X vale 0. Es decir, del estado interno 01 pasamos al 10, cuando X=0.
- Estado de transición 4, partiendo de los estados 1, 2 ó 3 con variables internas (instante t) Q1=0 y Q2=0, Q1=0 y Q2=1 ó Q1=1 y Q2=0, se pasa al estado 4 con variables internas (instante t+1) Q1=1 y Q2=1, si a la señal de reloj la entrada X vale 1. Es decir, de los estados internos 00, 10 ó 01 pasamos al 11, cuando X=1.
- Estado de transición 1, partiendo del estado 3 con variables internas (instante t) Q1=1 y Q2=0 se pasa al estado 1 con variables internas (instante t+1) Q1=0 y Q2=0, si a la señal de reloj la entrada X vale 0. Es decir, del estado interno 10 pasamos al 00, cuando X=0.
- Estado estable 4, estando el sistema en el estado Q1=1 y Q2=1 y la variable de entrada X permanece en 1 a cada señal de reloj, el estado 11 se mantiene.
Del diagrama de estados podemos construir la tabla de codificación de estados.
| ESTADOS | ENTRADA X | VARIABLES INTERNAS | ||
|---|---|---|---|---|
0 |
1 |
Q1 |
Q2 |
|
1 |
2 |
4 |
0 |
0 |
2 |
3 |
4 |
0 |
1 |
3 |
1 |
4 |
1 |
0 |
4 |
2 |
(4) |
1 |
1 |
Para construir la tabla de excitación del sistema, se crea una tabla de verdad donde las entradas son la entrada X y las variables internas en el estado de partida o instante anterior t. Las salidas son las variables internas en el estado posterior t+1. Si el sistema se diseña con biestables JK, la salidas estarán en función de J1, K1, J2 y K2. Sabemos que la tabla de transiciones de este biestable es:
| J | K | Q antes | Q después |
|---|---|---|---|
0 |
X |
0 |
0 |
1 |
X |
0 |
1 |
X |
1 |
1 |
0 |
X |
0 |
1 |
1 |
A partir de la tabla de codificación de estados y la tabla de transiciones del biestable JK, completamos la tabla de excitación del sistema:
| ESTADOS | ENTRADA | VARIABLES INTERNAS (instante t) | VARIABLES INTERNAS (instante t+1) | BIESTABLES JK | |||||
|---|---|---|---|---|---|---|---|---|---|
X |
Q1 |
Q2 |
Q1 |
Q2 |
J1 |
K1 |
J2 |
K2 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
X |
1 |
X |
2 |
0 |
0 |
1 |
1 |
0 |
1 |
X |
X |
1 |
3 |
0 |
1 |
0 |
0 |
0 |
X |
1 |
0 |
X |
4 |
0 |
1 |
1 |
0 |
1 |
X |
1 |
X |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
X |
1 |
X |
2 |
1 |
0 |
1 |
1 |
1 |
1 |
X |
X |
0 |
3 |
1 |
1 |
0 |
1 |
1 |
X |
0 |
1 |
X |
4 |
1 |
1 |
1 |
1 |
1 |
X |
0 |
X |
0 |
Para obtener las ecuaciones lógicas de salida realizamos los mapas de Karnaugh de J1, K1, J2 y K2, a partir de las entradas de la tabla de excitación: X, Q1 y Q2.
Las ecuaciones lógicas de salida son:
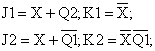
A partir de estas expresiones se obtiene el esquema del circuito lógico:
Cuál de las siguientes expresiones no corresponde con la entrada que necesita el biestable de tipo T(Q1) del diagrama de estados anterior.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Si el sistema se diseña con biestables T, sabemos que la tabla de transiciones de este biestable es:
| T | Q antes | Q después |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
La tabla de excitación del sistema secuencial del problema es:
| ESTADOS | ENTRADA | VARIABLES INTERNAS (instante t) | VARIABLES INTERNAS (instante t+1) | BIESTABLES T | |||
|---|---|---|---|---|---|---|---|
X |
Q1 |
Q2 |
Q1 |
Q2 |
T1 |
T2 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
3 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
4 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
3 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
4 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Si realizamos los mapas de Karnaugh de la variable T1 en función de Q1 y Q2:
a) ![]()
Por tanto, la respuesta es correcta.
b) ![]()
Por tanto, la respuesta es correcta.
c) ![]()
Por tanto, la respuesta es correcta.
d) ![]()
Al seleccionar dos ceros para obtener el resultado y dejar sin seleccionar un 1, la respuesta no es correcta.
Sabiendo que D1 y D2 son las entradas que necesitan dos biestables de tipo D para responder de acuerdo al diagrama de estados anterior, indique cuál de las siguientes expresiones es cierta.
a) T1+T2 = 1
b) T1+D1 = 1
c) T1+D2 = 1
d) T1+T2 = D1+D2
Si el sistema se diseña con biestables D, sabemos que la tabla de transiciones de este biestable es:
| D | Q antes | Q después |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
La tabla de excitación del sistema secuencial del problema es:
| ESTADOS | ENTRADA | VARIABLES INTERNAS (instante t) | VARIABLES INTERNAS (instante t+1) | BIESTABLES T | BIESTABLES D | ||||
|---|---|---|---|---|---|---|---|---|---|
X |
Q1 |
Q2 |
Q1 |
Q2 |
T1 |
T2 |
D1 |
D2 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
2 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
3 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
4 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
a) T1 + T2 = 1, no es correcto, ya que en la última fila de la tabla de excitación T1=0 y T2=0.
b) T1+D1 = 1, tampoco es correcto, ya que en la primera fila de la tabla de excitación T1=0 y D1=0.
c) T1+D2 = 1, si es correcto, ya que en todas las filas una de las dos variables es 1 ó las dos.
d) T1+T2 = D1+D2, no es correcto, ya que en la fila 3: T1+T2 = 1 y D1+D2 = 0.
Considerando que se han utilizado biestables tipo D en el diseño del sistema al que hace referencia el diagrama de estados anterior, indique cuál es la ecuación lógica de D1.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Si el sistema se diseña con biestables D, sabemos que la tabla de transiciones de este biestable es:
| D | Q antes | Q después |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
La tabla de excitación del sistema secuencial del problema es:
| ESTADOS | ENTRADA | VARIABLES INTERNAS (instante t) | VARIABLES INTERNAS (instante t+1) | BIESTABLES D | |||
|---|---|---|---|---|---|---|---|
X |
Q1 |
Q2 |
Q1 |
Q2 |
D1 |
D2 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
2 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
4 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Si realizamos el mapa de Karnaugh de la variable D1 en función de Q1 y Q2:
La respuesta correcta es:
a) ![]()