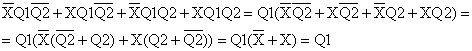
En los horizontales de la izquierda es Q1 quien cambia:
EJERCICIO 12 (Examen del Plan Nuevo Electrónica Digital y Electrónica Básica Digital Junio 2006/7 1ª Semana).
Tenemos el siguiente sistema secuencial representado por el diagrama de estados de la figura, con una entrada X y una salida Y y unas variables de estado Q1 y Q2. Se pide obtener la tabla de excitación, las ecuaciones lógicas de salida y el circuito lógico.
Si el sistema indicado en el diagrama de estados anterior, se diseña con biestables tipo JK, indique cuál de las siguientes afirmaciones es falsa.
a) Se puede hacer iguales las señales J1 e Y.
b) Se puede hacer K1 = 1.
c) Se puede hacer K1 = Q1.
d) Se puede hacer K1 = X.
Indique cuál de las siguientes expresiones es correcta.
a) J2 = XQ2
b) J1 = XQ1Q2
c) J1 = X
d) J1 = K1 = Q1 + XQ2
Indique cuál es el valor de Y.
a) Y = XQ1Q2
b) Y = Q1 + XQ2
c) Y = XQ1
d) Y = XQ2
SOLUCIÓN:
El diagrama de estado por el método de Mealy representa el funcionamiento de un circuito secuencial síncrono:
- Los estados internos del sistema, representados por las posibles combinaciones de las variables internas, están encerrados en un círculo. En nuestro problema hay tres estados internos diferentes representados por las combinaciones de Q1 y Q2.
- Las transiciones o cambios en el circuito al variar las entradas son las flechas que van de un círculo a otro. Estas transiciones se producen en cada señal de reloj.
- Sobre cada flecha se anota la combinación de entradas en la transición y, separadas por una barra, las salidas. En nuestro problema la entrada es X y la salida Y, se representa en el diagrama (X/Y). Las salidas dependen de las variables internas y de las entradas.
Observamos que hay dos estados estables (se mantiene el sistema en el mismo estado aunque se vayan produciendo pulsos de reloj), que son:
- Estado estable (1), con entrada X=0 y variables internas (instante t) Q1=0 y Q2=0, la salida es Y=0 y se pasa a variables internas (instante t+1) Q1=0 y Q2=0. Es decir, el estado interno 00 permanece.
- Estado estable (2), con entrada X=0 y variables internas (instante t) Q1=0 y Q2=1, la salida es Y=0 y se pasa a variables internas (instante t+1) Q1=0 y Q2=1. Es decir, el estado interno 01 permanece.
Hay 4 estados inestables o transiciones (cambia el estado con cada señal de reloj):
- Estado de transición 2, partiendo del estado estable (1) con variables internas (instante t) Q1=0 y Q2=0 al cambiar la entrada a 1, la salida es Y=0 y se pasa a variables internas (instante t+1) Q1=0 y Q2=1. Es decir, del estado interno 00 pasamos al 01.
- Estado de transición 3, partiendo del estado estable (2) con variables internas (instante t) Q1=0 y Q2=1 al cambiar la entrada a 1, la salida es Y=1 y se pasa a variables internas (instante t+1) Q1=1 y Q2=1. Es decir, del estado interno 01 pasamos al 11.
- Estado de transición 1, partiendo del estado inestable 3 con variables internas (instante t) Q1=1 y Q2=1 al cambiar la entrada a 1, la salida es Y=1 y se pasa a variables internas (instante t+1) Q1=0 y Q2=0. Es decir, del estado interno 11 pasamos al 00.
- Estado de transición 2, partiendo del estado inestable 3 con variables internas (instante t) Q1=1 y Q2=1 al cambiar la entrada a 0, la salida es Y=1 y se pasa a variables internas (instante t+1) Q1=0 y Q2=1. Es decir, del estado interno 11 pasamos al 01.
Vemos que hay dos estados de transición que se llaman 2, ya que llevan al mismo estado interno codificado con las variables internas por 01, pero sus estados origen son diferentes, así como sus salidas. Esto puede representarse en la llamada tabla de fases:
| ESTADOS ORIGEN | ENTRADA X | |
|---|---|---|
0 |
1 |
|
1 |
(1)/0 |
2/0 |
2 |
(2)/0 |
3/1 |
3 |
2/1 |
1/1 |
En la columna de la izquierda está el estado origen en el instante t (estado 1 combinación de variables internas Q1=0 Q2=0; estado 2 Q1=0 Q2=1; estado 3 Q1=1 Q2=1). En las columnas de la derecha se indica los estados a los que se llega (instante t+1) y la salida correspondiente, al cambiar la variable de entrada X. Por ejemplo, (1)/0 significa que llegamos al estado estable (1) y la salida es Y=0; 2/1 significa que llegamos al estado estable de transición 2 y la salida es Y=1. Los estados internos (es decir, las variables internas del sistema) van cambiando en cada pulso de reloj según el estado interno origen y la entrada. La salida cambia según el estado interno y la entrada del sistema sin necesidad de pulso de reloj.
De este diagrama podemos sacar la tabla de excitación del circuito de la siguiente manera:
| ESTADOS | ENTRADA | VARIABLES INTERNAS (instante t) | VARIABLES INTERNAS (instante t+1) | SALIDA | ||
|---|---|---|---|---|---|---|
X |
Q1 |
Q2 |
Q1 |
Q2 |
Y |
|
(1)/0 |
0 |
0 |
0 |
0 |
0 |
0 |
2/0 |
1 |
0 |
0 |
0 |
1 |
0 |
(2)/0 |
0 |
0 |
1 |
0 |
1 |
0 |
3/1 |
1 |
0 |
1 |
1 |
1 |
1 |
2/1 |
0 |
1 |
1 |
0 |
1 |
1 |
1/1 |
1 |
1 |
1 |
0 |
0 |
1 |
Para obtener las ecuaciones lógicas de salida, realizamos a partir de la Tabla de Verdad las simplificaciones con el mapa de karnaugh de la salida Y, y de las variables internas (en el instante t+1) Q1 y Q2.
Recordatorio del mapa de Karnaugh: en una tabla colocamos las combinaciones de la entrada X y las variables internas Q1 (antes) en una fila y Q2 (antes) en la columna. Las combinaciones de X y Q1 no pueden cambiar de estado lógico las dos a la vez en dos columnas consecutivas del mapa.
| Q2 | XQ1 | 00 | 01 | 11 | 10 |
|---|---|---|---|---|---|
| 0 |
|||||
1 |
|||||
Simplificación para Y: se colocan los valores de Y de la tabla de verdad en las celdas correspondientes del mapa de Karnaugh. En las combinaciones de las variables que la salida no es conocida o no se puede dar, se coloca una X (salida indeterminada). El mapa de Karnaugh no es más que la Tabla de Verdad dispuesta de otra manera.
Simplificación: seleccionamos los "1"s del mapa de tal manera que los asociemos adyacentes en potencias de 2 ( 1, 2, 4, 8, etc), con las asociaciones más grandes posibles y la menor cantidad de ellas, sin dejar ningún "1" sin seleccionar. Los "1"s pueden pertenecer a varias asociaciones y las dos columnas de los extremos son adyacentes entre sí. Las "X"s se pueden tomar como "1"s ó "0"s según nos convenga.
En las asociaciones elegidas las entradas que cambian de estado se eliminan de la combinación:
En los cuatro "1"s la X y Q2 pasan de "0" a "1", y no cambia Q1, tenemos:
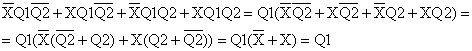
En los horizontales de la izquierda es Q1 quien cambia:
![]()
Por tanto, la ecución lógica de Y simplificada es:
Y=Q1+XQ2
Simplificación para Q1 y Q2:
La ecuación lógica de Q1 es:
|
La ecuación lógica de Q2 es:
|
Vemos que Q1 no tiene posible simplificación y en Q2 en los "1"s horizontales cambia Q1 y en los verticales Q2.
Como las variables internas del sistema (Q1 y Q2) van cambiando en cada pulso de reloj según el estado interno origen y la entrada, tendremos que realizar el mapa de Karnaugh para dichas variables añadiendo la entrada de reloj, para realizar el circuito lógico:
La ecuación lógica de Q1 es:
|
La ecuación lógica de Q2 es:
|
La salida no depende del pulso de reloj, sólo de las variables internas y la entrada, así se queda: Y=Q1+XQ2
El circuito lógico es el siguiente:
Si el sistema indicado en el diagrama de estados anterior, se diseña con biestables tipo JK, indique cuál de las siguientes afirmaciones es falsa.
a) Se puede hacer iguales las señales J1 e Y.
b) Se puede hacer K1 = 1.
c) Se puede hacer K1 = Q1.
d) Se puede hacer K1 = X.
La tabla de verdad de los biestables JK es:
| J | K | Q antes | Q después |
|---|---|---|---|
0 |
X |
0 |
0 |
1 |
X |
0 |
1 |
X |
1 |
1 |
0 |
X |
0 |
1 |
1 |
Si utilizamos biestables JK para el circuito, tenemos la siguiente tabla de verdad para las variables internas:
| ESTADOS | ENTRADA | VARIABLES INTERNAS (instante t) | VARIABLES INTERNAS (instante t+1) | BIESTABLES JK | |||||
|---|---|---|---|---|---|---|---|---|---|
X |
Q1 |
Q2 |
Q1 |
Q2 |
J1 |
K1 |
J2 |
K2 |
|
(1)/0 |
0 |
0 |
0 |
0 |
0 |
0 |
X |
0 |
X |
2/0 |
1 |
0 |
0 |
0 |
1 |
0 |
X |
1 |
X |
(2)/0 |
0 |
0 |
1 |
0 |
1 |
0 |
X |
X |
0 |
3/1 |
1 |
0 |
1 |
1 |
1 |
1 |
X |
X |
0 |
2/1 |
0 |
1 |
1 |
0 |
1 |
X |
1 |
X |
0 |
1/1 |
1 |
1 |
1 |
0 |
0 |
X |
1 |
X |
1 |
Vamos a realizar las simplificaciones de cada variable interna y de las salidas por medio de los mapas de Karnaugh. Las entradas del mapa serán la entrada X y las variables internas Q1 y Q2. Iremos comprobando cada una de las afirmaciones:
a) Se puede hacer iguales las señales J1 e Y.
Sabemos que Y=Q1+XQ2, vamos a ver en el mapa de karnaugh de J1 si podemos asociar todos los unos para dar esta combinación:
Si es posible, luego la afirmación es cierta.
b) Se puede hacer K1 = 1. En el mapa de karnaugh de K1 podemos asociar todos los unos para dar esta combinación:
c) Se puede hacer K1 = Q1. En el mapa de karnaugh de K1 podemos asociar todos los unos para dar esta combinación:
d) Se puede hacer K1 = X. Vemos que en el mapa de karnaugh de K1 no podemos asociar todos los unos para dar esta combinación, nos quedaría sin asociar un uno. La afirmación es falsa.
Indique cuál de las siguientes expresiones es correcta.
a) J2 = XQ2
b) J1 = XQ1Q2
c) J1 = X
d) J1 = K1 = Q1 + XQ2.
a) J2 = XQ2. Vemos que en el mapa de karnaugh de J2 no podemos asociar todos los unos para dar esta combinación, nos quedaría sin asociar un uno. La afirmación es falsa.
b) J1 = XQ1Q2. Vemos que en el mapa de karnaugh de J1 no podemos asociar todos los unos para dar esta combinación, nos quedaría sin asociar un uno. La afirmación es falsa.
c) J1 = X. Vemos que en el mapa de karnaugh de J1 si asociamos los unos para dar esta combinación, nos quedaría un cero dentro. La afirmación es falsa.
d) J1 = K1 = Q1 + XQ2. En los mapas de karnaugh de K1 y J1 podemos asociar todos los unos para dar esta combinación. Por tanto, la afirmación es cierta.
Indique cuál es el valor de Y.
a) Y = XQ1Q2
b) Y = Q1 + XQ2
c) Y = XQ1
d) Y = XQ2
El valor de Y como hemos visto anteriormente es b) Y = Q1 + XQ2.