EJERCICIO 11 (Examen del Plan Antiguo Electrónica II Junio 2006/7 2ª Prueba Personal 2ª Semana).
Un sistema tiene dos entradas E1 y E2, y dos salidas S1 y S2, debiendo cumplir las siguientes especificaciones:
- En estado de reposo las salidas deben ser 1, 1.
- Si se suceden al menos dos combinaciones de entradas 1,1 las salidas deben ser 0,0.
- Si después de estas dos entradas se sucede la combinación 0,0, las salidas deben ser 0,1.
- Dos variables no pueden cambiar de estado simultáneamente.
Diseñe un circuito síncrono que cumpla estas características.
SOLUCIÓN:
Se va a resolver el problema como un sistema secuencial síncrono, para ello se seguirán los siguientes pasos:
1) Identificación de las variables de entrada y salida.
En el enunciado del problema se piden dos salidas S1 y S2 y dice que el sistema tiene dos entradas E1 y E2.
2) Construcción de la tabla de estados. Es una representación, mediante una tabla, de la secuencia de estados por los que evoluciona el sistema. Los pasos a seguir para su construcción son los siguientes:
a) La tabla de fases tendrá tantas columnas como combinaciones de entrada del sistema, añadiendo las columnas por cada una de las salidas y una columna que indica el estado en el que se encuentra el sistema. En este problema se tienen dos entradas que generan 4 combinaciones y dos salidas; por tanto, se tienen 7 columnas.
b) Las filas de la tabla van creándose según van apareciendo nuevos estados. En cada fila se representa un sólo estado estable del circuito, mediante un número encerrado entre paréntesis, situado en la columna correspondiente a la combinación de variables de entrada que le dan lugar.
c) La salida que produce dicho estado se escribe en la misma fila, en la columna de la salida.
d) En la misma fila se escriben las transiciones a otros estados, que se producen cuando varían las entradas (éstas no pueden variar dos o más a la vez), con el mismo número del estado destino de la transición, pero sin encerrar entre paréntesis, y situados en la columna de la nueva combinación de entradas.
e) Cuando todas las transiciones vayan ya hacia estados anteriores, la tabla está completa.
Tabla de estados
| ESTADOS | ENTRADAS E1E2 | SALIDAS | EXPLICACIÓN DE CADA ESTADO | ||||
|---|---|---|---|---|---|---|---|
00 |
01 |
11 |
10 |
S1 |
S2 |
||
1 |
(1) |
2 |
- |
3 |
1 |
1 |
Estado de reposo |
2 |
1 |
(2) |
4 |
- |
1 |
1 |
Estado no cambia el estado de reposo |
3 |
1 |
- |
4 |
(3) |
1 |
1 |
Estado no cambia el estado de reposo |
Antes de proseguir la tabla, vemos que los estados 2 y 3 son pseudoequivalentes, ya que coinciden sus salidas y sus transiciones (estados equivalentes) y hay estados imposibles. Por tanto, eliminamos uno de ellos y reestructuramos la tabla. En realidad, los estados con las entradas 01 y 10 que vuelvan a aparecer serán pseudoequivalentes de nuevo , ya que estas entradas no afectan sobre la salida y sus transiciones a otra combinación de entradas son las mismas y no modificarán las salidas. Parecería que el estado 1 fuera pseudoequivalente con el 2, pero si lo fuera el sistema no evolucionaría más, ya que desde entradas 00 no se puede pasar a entradas 11 si no es por transiciones 01 ó 10.
| ESTADOS | ENTRADAS E1E2 | SALIDAS | EXPLICACIÓN DE CADA ESTADO | ||||
|---|---|---|---|---|---|---|---|
00 |
01 |
11 |
10 |
S1 |
S2 |
||
1 |
(1) |
2 |
- |
2 |
1 |
1 |
Estado de reposo |
2 |
1 |
(2) |
3 |
(2) |
1 |
1 |
Estado no cambia el estado de reposo, pero puede evolucionar a las entradas 11 |
3 |
- |
2 |
4 |
2 |
1 |
1 |
estado de transición, entradas 11 por primera vez |
4 |
- |
5 |
4 |
5 |
0 |
0 |
Dos entradas seguidas o más 11 cambian las salidas a 00 |
5 |
6 |
(5) |
4 |
(5) |
0 |
0 |
Estado no cambia el estado anterior, pero puede evolucionar a las entradas 00 |
6 |
(6) |
7 |
- |
7 |
0 |
1 |
Después de dos entradas 11, se produce 00 |
7 |
6 |
(7) |
8 |
(7) |
0 |
1 |
Estado no cambia el estado anterior, pero puede evolucionar a las entradas 11 |
8 |
- |
7 |
4 |
7 |
0 |
0 |
estado de transición, entradas 11 por primera vez después de venir de salidas 01 |
3) Fusión de la tabla de estados. Dos filas de la tabla de estados son fusionables si coinciden en sus columnas el número de los estados o estado y guión. No es necesario que coincidan sus salidas, aunque si esto ocurre, la salida depende sólo de los estados internos (Modelo de Moore). En la tabla de fusión, las columnas llevarán:
a) el número del estado con paréntesis si en alguna de las filas fusionadas este estado tenía paréntesis,
b) el número del estado sin paréntesis si en ninguna de las filas fusionadas este estado tenía paréntesis, pero aparece el número sin paréntesis,
c) guión si en todas las filas fusionadas hay guiones.
En este problema se pueden fusionar los estados 1 y 2; 4 y 5; 6 y 7, dando lugar a la siguiente tabla de fusión:
| ESTADOS | ENTRADAS E1E2 | |||
|---|---|---|---|---|
00 |
01 |
11 |
10 |
|
1-2 |
(1) |
(2) |
3 |
(2) |
3 |
- |
2 |
4 |
2 |
4-5 |
6 |
(5) |
(4) |
(5) |
6-7 |
(6) |
(7) |
8 |
(7) |
8 |
- |
7 |
4 |
7 |
Cada línea de la tabla de fusión surge para discriminar entre dos estados que tienen la misma combinación de entradas, pero diferente salida: los estados 2 y 7 tienen la misma combinación de entrada 01 ó 10, pero la salida del estado 2 es 11 y la del estado 7 es 01.
4) Codificación de estados internos. El número de variables internas (n) depende del número de filas de la tabla de fusión (N) cumpliéndose la siguiente expresión: 2n-1<N<=2n ; en este caso N=5 y tres variables internas Q0, Q1 y Q2 son necesarias para la discriminación de los estados.
Tabla de fusión codificada.
Partiendo de la tabla de fusión se asigna a cada línea un estado interno.
Se pueden asignar dos de las variables internas (por ejemplo Q1 y Q0) de modo que coincidan con las salidas del circuito, reduciéndose las ecuaciones de salida y por tanto el circuito, dando lugar a un caso particular del autómata finito Mealy, llamado Moore:
| ESTADOS | ENTRADAS E1E2 | SALIDAS | VARIABLES INTERNAS | ||||||
|---|---|---|---|---|---|---|---|---|---|
00 |
01 |
11 |
10 |
S1 |
S2 |
Q2 | Q1 | Q0 | |
1-2 |
(1) |
(2) |
3 |
(2) |
1 |
1 |
1 |
1 |
1 |
3 |
- |
2 |
4 |
2 |
1 |
1 |
0 |
1 |
1 |
4-5 |
6 |
(5) |
(4) |
(5) |
0 |
0 |
0 |
0 |
0 |
6-7 |
(6) |
(7) |
8 |
(7) |
0 |
1 |
0 |
0 |
1 |
8 |
- |
7 |
4 |
7 |
0 |
1 |
1 |
0 |
1 |
5) Tabla de excitación. Se construye a partir de la tabla de fusión codificada. Se colocan en cada fila cada uno de los estados estables y de transición que aparecen en la tabla de fusión codificada. En las columnas se tienen como entradas las entradas del sistema (E1 y E2 ) y el valor de las variables internas en ese instante (Qt); en las salidas están la salidas del sistema (S1 y S2) y el valor de las variables internas al siguiente instante (Qt+1). Se rellena la tabla con la combinación de entradas y estado interno (Qt) presente para cada estado (estable o de transición). En los estados estables la variables internas antes es igual a la variables internas después Qt+1 = Qt. En los estados de transición la variables internas cambian al valor que tendrá en su estado posterior correspondiente.
Con biestables JK, la tabla de transiciones es:
| J | K | Q antes | Q después |
|---|---|---|---|
0 |
X |
0 |
0 |
1 |
X |
0 |
1 |
X |
1 |
1 |
0 |
X |
0 |
1 |
1 |
Así, la tabla de excitación queda:
| ESTADOS | ENTRADAS | SALIDAS | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
E1 |
E2 |
Q2(t) |
Q1(t) |
Q0(t) |
Q2(t+1) | Q1(t+1) | Q0(t+1) |
J2 | K2 | J1 | K1 | J0 | K0 |
S1 | S2 | |
(1) |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
X |
0 |
X |
0 |
X |
0 |
1 |
1 |
(2) |
0 1 |
1 0 |
1 |
1 |
1 |
1 |
1 |
1 |
X |
0 |
X |
0 |
X |
0 |
1 |
1 |
2 |
0 1 |
1 0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
X |
X |
0 |
X |
0 |
1 |
1 |
3 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
X |
1 |
X |
0 |
X |
0 |
1 |
1 |
(4) |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X |
0 |
X |
0 |
X |
0 |
0 |
4 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
X |
X |
1 |
X |
1 |
0 |
0 |
4 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
X |
1 |
0 |
X |
X |
1 |
0 |
0 |
5 |
0 1 |
1 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X |
0 |
X |
0 |
X |
0 |
0 |
(6) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
X |
0 |
X |
X |
0 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
X |
0 |
X |
1 |
X |
0 |
1 |
(7) |
0 1 |
1 0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
X |
0 |
X |
X |
0 |
0 |
1 |
7 |
0 1 |
1 0 |
1 |
0 |
1 |
0 |
0 |
1 |
X |
1 |
0 |
X |
X |
0 |
0 |
1 |
8 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
X |
0 |
X |
X |
0 |
0 |
1 |
6) Ecuaciones lógicas de las salidas y de las variables internas. De la tabla de excitación se sacan los mapas de Karnaugh para las salidas y las variables internas dadas por los biestables JK.
Las ecuaciones lógicas deducidas de las simplificaciones del mapa de Karnaugh son:
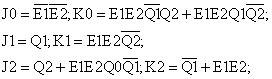
En el circuito hay que inicializar Q0, Q1 y Q2 a 1 para empezar la secuencia correctamente.