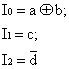
JUNIO 2006
a) Obtenga una expresión de conmutación en función de a, b, c y d de la señal lógica z mostrada en la figura.
b) Obtenga la tabla de verdad de la función lógica z(a,b,c,d) que realiza el circuito de la figura.
SOLUCIÓN:
Analizando el circuito nos encontramos los siguientes componentes:
Una puerta EXOR cuyas entradas son a y b y su salida es la entrada I0 del decodificador.
| a | b | I0 |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Una puerta NAND cuyas entradas son d y d, por lo que la salida es la inversa de d, que entrará como I2 en el decodificador.
| d | d | I2 |
|---|---|---|
0 |
0 |
1 |
1 |
1 |
0 |
Un DECODIFICADOR de 3 entradas y 8 salidas. Las entradas son:
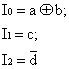
La salidas del decodificador S2, S4, S5 y S7 entran en una puerta OR para dar la señal de salida z, por tanto, la ecuación de z es:
z = S2 + S4 + S5 + S7
Las salidas S2, S4, S5 y S7 corresponden a las siguientes combinaciones de las entradas I 0, I 1 y I 2:
FUNCIONAMIENTO DE UN DECODIFICADOR 3:8.
La tabla de verdad de z en función de a, b, c y d queda así:
| ENTRADAS | ENTRADAS DECODIFICADOR | SALIDA | |||||
|---|---|---|---|---|---|---|---|
a |
b |
c |
d |
I1= c |
z |
||
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
Una expresión de z en función de a, b, c y d podemos deducirla de la tabla de verdad, sumando las combinaciones cuya salida es "1":
![]()
El funcionamiento del circuito es: