EJERCICIO 33 (Examen del Plan Nuevo Electrónica Digital Junio 2007/8 2 ª Semana)
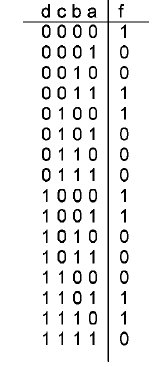
Dada la siguiente Tabla de Verdad:
Determine cuál es su función canónica en minitérminos (minterms):
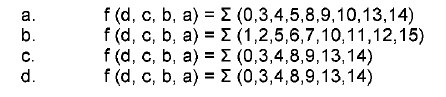
Determine cuál es su función canónica en maxitérminos (maxterms):
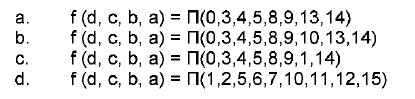
Simplifique la expresión por el método de Karnaugh:
SOLUCIÓN:
Una función lógica se puede expresar mediante dos formas canónicas:
a) Suma de minterms.
b) Producto de maxterms.
a) Los minitérminos (minterms) son el producto de todas las entradas, asociando la variable natural (a, b, c, d) si toma el valor 1 en la tabla de verdad y negada (a´= 
,b´= 
, c´= 
, d´= 
) si toma el valor 0. Se representa por mi los productos canónicos, con "i" igual al valor decimal de la combinación binaria que se obtiene al sustituir por 1 las variables que aparecen (en el producto canónico) en forma natural y por 0 a las que lo hacen en forma negada.
b) Los maxitérminos (Maxterms) son la suma de todas las entradas, asociando la variable negada (, , , ) si toma el valor 1 en la tabla de verdad y sin negar (a, b, c, d) si toma el valor 0. Se representa por M i las sumas canónicas, con "i" igual significado que en los productos canónicos.
En la siguiente tabla tenemos los minitérminos y los maxitérminos para cuatro entradas a, b, c y d, así como el valor de la salida f:
| d | c | b | a | Maxterms | minterms | f |
|---|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
 |
 |
1 |
0 |
0 |
0 |
1 |
 |
 |
0 |
0 |
0 |
1 |
0 |
 |
 |
0 |
0 |
0 |
1 |
1 |
 |
 |
1 |
0 |
1 |
0 |
0 |
 |
 |
1 |
0 |
1 |
0 |
1 |
 |
 |
0 |
0 |
1 |
1 |
0 |
 |
 |
0 |
0 |
1 |
1 |
1 |
 |
 |
0 |
1 |
0 |
0 |
0 |
 |
 |
1 |
1 |
0 |
0 |
1 |
 |
 |
1 |
1 |
0 |
1 |
0 |
 |
 |
0 |
1 |
0 |
1 |
1 |
 |
 |
0 |
1 |
1 |
0 |
0 |
 |
 |
0 |
1 |
1 |
0 |
1 |
 |
 |
1 |
1 |
1 |
1 |
0 |
 |
 |
1 |
1 |
1 |
1 |
1 |
 |
 |
0 |
La función lógica se puede expresar como suma de minitérminos (minterms), donde aparecerán aquellos que en la tabla de verdad la salida f valga "1":
f = m0 + m3 + m4 + m8+ m9 + m13 + m14
por tanto, observando la tabla, la respuesta correcta es:
c) 
La función lógica se puede expresar también, como producto de maxitérminos (Maxterms), donde aparecerán aquellos que en la tabla de verdad la salida f valga "0":
f = M 0M 3M4M 5M 8M9M 10M 13M 14
por tanto, la respuesta correcta es:
b) 
El mapa de Karnaugh es la tabla de verdad dispuesta de otra manera: en una tabla colocamos las combinaciones de las entradas a y b en una columna y las de c y d en la fila. Las combinaciones de c y d no pueden cambiar de estado lógico las dos a la vez en dos filas consecutivas del mapa y tampoco las de a y b.
Esta es la representación del mapa de Karnaugh con minterms.
| dc | ba | 00 |
01 |
11 |
10 |
|---|---|---|---|---|---|
| 00 |
m0 |
m1 |
m3 |
m2 |
|
01 |
m4 |
m5 |
m7 |
m6 |
|
| 11 | m12 |
m13 |
m15 |
m14 |
|
| 10 | m8 |
m9 |
m11 |
m10 |
|
Simplificación por unos: seleccionamos los "1"s del mapa de tal manera que los asociemos adyacentes en potencias de 2 ( 1, 2, 4, 8, etc), con las asociaciones más grandes posibles y la menor cantidad de ellas, sin dejar ningún "1" sin seleccionar. Los "1"s pueden pertenecer a varias asociaciones y las dos columnas (y filas) de los extremos son adyacentes entre sí.
En las asociaciones elegidas las entradas que cambian de estado se eliminan de la combinación: En los dos unos verticales superiores de la izquierda cambia c: En los dos unos horizontales inferiores cambia a:
En los dos unos verticales inferiores cambia c:
Los otros dos unos no podemos simplificarlos y aparecen los términos enteros:
|
Por tanto, la función lógica f simplificada es la respuesta d):
y 