EJERCICIO 2
Minimice e implemente con decodificadores de cuatro entradas un circuito detector de paridad impar (número de unos impar) de un número digital de 5 entradas.
SOLUCIÓN
Construimos la tabla de verdad de en número de 5 dígitos asignando como entradas E, D, C, B Y A; y salida un uno donde haya un número impar de unos:
| ENTRADAS | SALIDA | ||||
|---|---|---|---|---|---|
E |
D |
C |
B |
A |
S |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Realizamos el mapa de Karnaugh para su simplificación: en una tabla colocamos las combinaciones de las entradas E y D en una columna y las de CBA en la fila. Las combinaciones de E y D no pueden cambiar de estado lógico las dos a la vez en dos filas consecutivas del mapa y tampoco las de C, B y A..
| ED | CBA | 000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 |
|---|---|---|---|---|---|---|---|---|---|
| 00 |
0 |
(1) |
0 |
(1) |
0 |
(1) |
0 |
(1) |
|
01 |
(1) |
0 |
(1) |
0 |
(1) |
0 |
(1) |
0 |
|
| 11 | 0 |
(1) |
0 |
(1) |
0 |
(1) |
0 |
(1) |
|
| 10 | (1) |
0 |
(1) |
0 |
(1) |
0 |
(1) |
0 |
|
Se colocan los valores de S de la tabla de verdad en las celdas correspondientes del mapa de Karnaugh. El mapa de Karnaugh no es más que la Tabla de Verdad dispuesta de otra manera.
Simplificación: seleccionamos los "1"s del mapa de tal manera que los asociemos adyacentes en potencias de 2 ( 1, 2, 4, 8, etc), con las asociaciones más grandes posibles y la menor cantidad de ellas, sin dejar ningún "1" sin seleccionar. Los "1"s pueden pertenecer a varias asociaciones y las dos columnas de los extremos son adyacentes entre sí, así como aquellas en las que sólo cambia un dígito (columnas de CBA: 000-010; 001-101; 011-111; 110-100).
Observamos en el mapa que todos los unos están en posiciones no adyacentes no pudiendo asociarlos entre sí; por tanto no hay posible simplificación.
Si tenemos que inplementar la función con decodificadores de cuatro entradas, vamos a ver como funcionan: para cada una de las combinaciones de las entradas sólo está activa una salida, la que tiene el valor decimal de las entradas en binario. Las demás salidas están a 0.
Si nuestras entradas D, C, B y A del problema son las que entran en un decodificador de cuatro entradas, vemos que para E=0 las combinaciones que dan 1 en la tabla de verdad son Q1, Q2, Q4, Q7, Q8, Q11, Q13 y Q14. Luego, podemos meter éstas en una puerta OR y la salida de esta OR con la entrada E negada (inversor) en una AND; y así tenemos los ocho primeros unos de la tabla (en rojo).
Para E=1 las combinaciones de D, C, B y A que dan 1 son las otras ocho: Q0, Q3, Q5, Q6, Q9, Q10, Q12 y Q15. Todas éstas entran en una OR y su salida con E a una AND. Así tenemos los ocho unos restantes de la tabla (en verde)
| ENTRADAS | SALIDA | |||||
|---|---|---|---|---|---|---|
E |
D |
C |
B |
A |
DECODIFICADOR |
S |
0 |
0 |
0 |
0 |
0 |
Q0 |
0 |
0 |
0 |
0 |
0 |
1 |
Q1 |
1 |
0 |
0 |
0 |
1 |
0 |
Q2 |
1 |
0 |
0 |
0 |
1 |
1 |
Q3 |
0 |
0 |
0 |
1 |
0 |
0 |
Q4 |
1 |
0 |
0 |
1 |
0 |
1 |
Q5 |
0 |
0 |
0 |
1 |
1 |
0 |
Q6 |
0 |
0 |
0 |
1 |
1 |
1 |
Q7 |
1 |
0 |
1 |
0 |
0 |
0 |
Q8 |
1 |
0 |
1 |
0 |
0 |
1 |
Q9 |
0 |
0 |
1 |
0 |
1 |
0 |
Q10 |
0 |
0 |
1 |
0 |
1 |
1 |
Q11 |
1 |
0 |
1 |
1 |
0 |
0 |
Q12 |
0 |
0 |
1 |
1 |
0 |
1 |
Q13 |
1 |
0 |
1 |
1 |
1 |
0 |
Q14 |
1 |
0 |
1 |
1 |
1 |
1 |
Q15 |
0 |
1 |
0 |
0 |
0 |
0 |
Q0 |
1 |
1 |
0 |
0 |
0 |
1 |
Q1 |
0 |
1 |
0 |
0 |
1 |
0 |
Q2 |
0 |
1 |
0 |
0 |
1 |
1 |
Q3 |
1 |
1 |
0 |
1 |
0 |
0 |
Q4 |
0 |
1 |
0 |
1 |
0 |
1 |
Q5 |
1 |
1 |
0 |
1 |
1 |
0 |
Q6 |
1 |
1 |
0 |
1 |
1 |
1 |
Q7 |
0 |
1 |
1 |
0 |
0 |
0 |
Q8 |
0 |
1 |
1 |
0 |
0 |
1 |
Q9 |
1 |
1 |
1 |
0 |
1 |
0 |
Q10 |
1 |
1 |
1 |
0 |
1 |
1 |
Q11 |
0 |
1 |
1 |
1 |
0 |
0 |
Q12 |
1 |
1 |
1 |
1 |
0 |
1 |
Q13 |
0 |
1 |
1 |
1 |
1 |
0 |
Q14 |
0 |
1 |
1 |
1 |
1 |
1 |
Q15 |
1 |
El circuito con decodificador será:
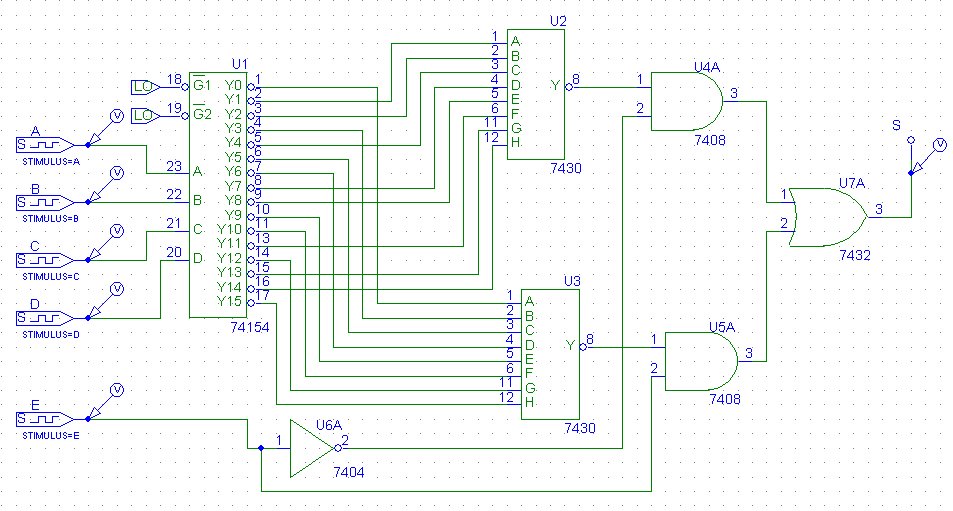
El esquema realizado con el programa DesignLab es el siguiente:
En el esquema realizado con el programa DesignLab, el componente 74154 debe tener las entradas 
y 
a 0 para funcionar como decodificador, con otras combinaciones funciona como multiplexor. Las salidas del decodificador están a nivel alto, excepto la correspondiente a la combinación de entrada que se decodifica, que está a nivel bajo. Por esto y como no hay en el programa puertas OR de ocho entradas, hemos realizado con puertas NAND de ocho entradas la misma función. Las variables Y son las negadas de Q.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
El análisis en el tiempo del circuito nos da el siguiente cronograma, que coincide con la tabla de verdad inicial. Para comprobarlo mueve el rectángulo rojo de la tabla con MOVER TABLA o mueve la línea roja del cronograma con MOVER CURSOR. Al pulsar el botón izquierdo del ratón el rectángulo y el cursor rojo se paran en la posición deseada. Para volver a moverlos pulsar MOVER TABLA o MOVER CURSOR. :